Don’t Bet on PME: A Tale of Public Market Equivalents and Their Limitations

You’re sitting across from a General Partner (GP) at a biotech-focused venture capital (VC) fund. They’re presenting their latest performance report, brimming with confidence. “We’ve achieved a PME ratio of 1.4,” the GP declares, leaning back with a satisfied smile. “This proves we’re outperforming public markets by 40%.”

You sip your coffee, nodding politely. A PME ratio greater than 1 certainly sounds impressive. But something about the claim feels too neat, too precise. You wonder: Is PME really the definitive measure of success for private funds, especially in complex sectors like VC and pharma?

What Are Public Market Equivalents (PME)?

PME—or Public Market Equivalents—are a method used to benchmark private fund performance against public market indices. One popular approach is the Kaplan-Schoar PME, which compares a fund’s cash flows to a hypothetical investment in a public market index:

$$
\text{PME Ratio} = \frac{\text{Discounted Distributions}}{\text{Discounted Contributions}}
$$

Where:

• Discounted Distributions: Cash flows distributed to Limited Partners (LPs) at time , discounted by the public market benchmark.
• Discounted Contributions: Cash flows contributed by LPs at time , discounted by the public market benchmark.
• : Return of the public market benchmark (e.g., S&P 500) at time .

A PME ratio greater than 1 suggests the fund outperformed public markets, while a ratio below 1 indicates underperformance.

Alex’s Investigation

Meet Alex, an LP evaluating a biotech-focused VC fund. The GP’s pitch is compelling: a PME ratio of 1.4 and claims of consistent outperformance. But Alex, a seasoned investor, decides to dig deeper. She starts by recalculating the PME ratio using the Kaplan-Schoar formula.

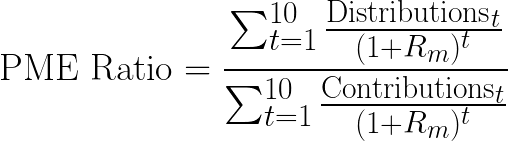
The numbers check out. The PME ratio is indeed 1.4. But as Alex examines the assumptions, she spots several red flags.

The Problem with PME

1. Assumption of Perfect Liquidity

PME assumes that cash flows can be reinvested in the public market index at the same rate of return. But Alex knows that private funds often involve long holding periods and illiquid assets. Reinvesting distributions is rarely straightforward, and the assumption of perfect liquidity doesn’t hold up.

2. Timing and the J-Curve Effect

Alex plots the fund’s cash flows and notices the familiar J-curve pattern:

• Early contributions are negative due to fees and investment costs.
• Positive distributions come much later, as portfolio companies mature and exit.

Public market indices, on the other hand, assume continuous compounding of returns. PME doesn’t account for this mismatch in timing, potentially overstating the fund’s performance.

3. Sector-Specific Challenges

In Venture Capital:

• Power-Law Distributions: Alex knows that VC returns are driven by a few “unicorns”—companies that generate outsized gains. The rest of the portfolio might underperform or fail entirely. Public market indices assume normally distributed returns, which don’t reflect this reality.

In Pharma:

• Binary Outcomes: Drug development relies on high-risk, binary events like clinical trial results. These outcomes don’t correlate with broader market movements, making PME comparisons misleading.

4. Choice of Benchmark

The GP used the Nasdaq Biotechnology Index as the benchmark, which makes sense for a biotech fund. But when Alex recalculates the PME ratio using the S&P 500, the ratio drops to 1.1. The fund still outperforms, but the margin is much narrower. This variability underscores how sensitive PME results are to the choice of benchmark.

Taleb’s Critique of PME

As Alex considers these limitations, she recalls Nassim Nicholas Taleb’s critique of simplified financial models in The Black Swan. Taleb warns against overreliance on metrics that assume stability and predictability in complex environments.

1. Ignoring Tail Risks:
   • PME measures average performance but overlooks the rare, extreme events that define returns in VC and pharma.
2. Reinvestment Assumptions:
   • PME assumes cash flows can be reinvested seamlessly at the benchmark rate. In illiquid markets, this is unrealistic.
3. False Precision:
   • Like beta, PME offers a veneer of mathematical rigor that can obscure its underlying flaws.

A Better Way Forward

Determined to find a more accurate way to evaluate the fund’s performance, Alex explores alternative approaches:

1. Customized Benchmarks

Instead of relying solely on public indices, Alex suggests creating customized benchmarks that reflect the fund’s specific focus:

• A biotech VC fund could benchmark against a weighted index of biotech stocks and public drug development companies.
• A multi-sector VC fund could use a composite index based on its sector allocations.

2. Internal Rate of Return (IRR)

While IRR has its own limitations, it accounts for the irregular cash flows of private funds. Alex recalculates the fund’s IRR:

$$
\text{IRR: The discount rate that makes the net present value (NPV) of all cash flows equal to zero.}
$$

3. Monte Carlo Simulations

Monte Carlo models can simulate thousands of scenarios to evaluate fund performance under varying market conditions:

$$
\text{Simulated PME Ratio} = \text{Average PME outcomes across simulated scenarios.}
$$

4. Extreme Value Theory (EVT)

To address tail risks, Alex applies EVT, which focuses on rare, high-impact events:

$$
P(X > x) \sim x^{-\alpha} \quad \text{for large x.}
$$

5. Portfolio Diversification Metrics

Alex evaluates the fund’s diversification across:

• Sectors: Balancing investments in oncology, neurology, and rare diseases.
• Stages: Spreading risk across early-stage and late-stage companies.
• Geographies: Reducing country-specific risks.

Conclusion

By the end of her analysis, Alex has a clearer picture of the fund’s performance. While PME offers a starting point, its limitations make it unsuitable as the sole measure of success for private funds. In complex, high-risk sectors like VC and pharma, alternative approaches provide a more nuanced understanding of risk and return.

Key Takeaways

1. PME is a useful benchmarking tool but must be used cautiously, especially in illiquid, high-risk sectors.
2. Alternative metrics like IRR, Monte Carlo simulations, EVT, and customized benchmarks offer a deeper understanding of fund performance.
3. Investors like Alex must dig beyond surface metrics to uncover the true drivers of risk and return in private markets.